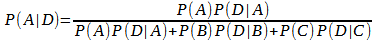RESOLVENDO UMA EQUAÇÃO INTEGRAL

Olá! É sempre um prestígio ter você aqui.

Nesta publicação, você aprenderá a resolver uma equação integral por meio de um exemplo*, seguindo seis passos.

Uma equação integral envolve uma função desconhecida e uma integral envolvendo essa mesma função.

Resolveremos a equação:

$y(x)=2+{\int }_2^x[t-\mathit{ty}(t)]\mathit{dt}$

(1)

1. Passo 1)Determinando uma condição inicial.

   Basta se lembrar de que a integral é nula quando os limites de integração são iguais. Assim, em x = 2, a equação (1) retorna y = 2.

2. Passo 2)Derivar a equação (1).

   A derivada de (1) é a derivada da constante 2, que é zero, somada à derivada da integral, que é igual ao integrando aplicando x à variável t, em razão do Teorema Fundamental do Cálculo:

$y\text{'}(x)=x-\mathit{xy}(x)$

(2)

1. Essa é uma equação separável. Portanto:

$y\text{'}(x)=x(1-y(x))$

(3)

Podemos reescrevê-la:

$\frac{y\text{'}(x)}{1-y(x)}=x$

(4)

Desde que essa expressão nos conduz a uma inconsistência, vamos escrevê-la como:

$\frac{y\text{'}(x)}{y(x)-1}=-x$

(5)

1. Passo 3)Integrar (5)

Do lado direito de (5), temos a derivada de

$\ln \text{|}y(x)-1\text{|}+C_0$

. Agrupando as constantes em uma só, temos:

$\ln \text{|}y(x)-1\text{|}=\frac{-x^2}{2}+C$

(6)

1. Passo 4)Determinar a constante C.

Basta usar nossa condição inicial, isto é, y(2) = 2.

$\ln \text{|}y(2)-1\text{|}=\frac{-2^2}{2}+C\to 0=\ln \text{|}2-1\text{|}=-2+C\to C=2$

1. Passo 5)Aplicar a exponencial a ambos os lados de (6).

A função exponencial é a inversa da função logarítmica natural. Assim:

$\text{|}y(x)-1\text{|}=e^{2-x^2/2}$

(7)

Desde que o lado direito é sempre positivo, podemos escrever:

$y(x)-1=e^{2-x^2/2}$

(8)

Por fim:

$y(x)=1+e^{2-x^2/2}$

(9)

2. Passo 6)Refaça os 5 passos anteriores, sem olhar pelo exemplo.

Desejo a você uma excelente aprendizagem, pois APRENDER É A NOSSA MELHOR HABILIDADE!

Siga-me no Instagram

Forte abraço e até brevíssimo!

* O exemplo dado aqui é o exercício 35 da seção 9.3 da nona edição do livro Cálculo, volume 2, de J. Stewart, D. Clegg, S. Watson, pela editora Cengage.

TEOREMA DE BAYES

 Olá! É sempre um prestígio ter você aqui.

Nesta publicação, você aprenderá sobre:

• teorema de Bayes; 
• independência entre eventos, 
• provas repetidas e independentes, 
• eventos mutuamente exclusivos.

Desejo a você uma boa aprendizagem!

A probabilidade condicionada, isto é, a probabilidade de um evento ocorrer dado que outro ocorreu, leva-nos à relação

Também podemos escrever

Assim, a interseção entre A e B podem ser dadas pelos produtos:

 Podemos também escrever:

 O resultado mais relevante, nesse contexto é o seguinte teorema:

 Por indução, tem-se que:

 sendo os A_i eventos quaisquer.

Calma! Vamos fazer com 3, primeiro?

 Tudo bem até aí? Perceba que temos mais uma interseção para “desmembrar”. Isto é:

Agora ficou mais fácil visualizar a expressão com n eventos.

Vamos a outro teorema de grande importância em probabilidade: o teorema de Bayes.

Considere que os eventos

 formem uma partição de um espaço amostral S. Isto significa que são mutuamente exclusivos, e que sua união resulta em S. Considere outro evento qualquer de S, digamos B. Então:

 Disso, segue-se que

E do Teorema da Multiplicação:

Sabemos ainda que, para qualquer evento A_i, a probabilidade condicional de A_i dado B é dada por:

 Fazendo as substituições adequadas, temos:

 Isto é, o Teorema de Bayes.

Vejamos alguns exemplos da utilidade desse teorema.

Primeiro exemplo: considere que três robôs – A, B, e C – são responsáveis por 50%, 30%, e 20% de todas as operações num pregão da bolsa de valores brasileira. As percentagens de operações com prejuízo desses robôs são 3%, 4% e 5%, nesta ordem. Se uma operação for escolhida aleatoriamente, qual a probabilidade de ela ter resultado em prejuízo?

Para início, você precisa enxergar as relações entre os eventos dados. Você sabe que a operação deve resultar em prejuízo, mas não sabe de que robô ela partiu. Portanto, devemos considerar a probabilidade conjunta das interseções entre “operação com prejuízo” e “partiu do robô Y”, para este resultado. Em símbolos, sendo D a “operação com prejuízo”:

Isto é:

 Segundo exemplo: dadas as condições do primeiro exemplo, foi escolhida aleatoriamente uma operação. Calcule a probabilidade de ela ter sido disparada pelo robô A.

Agora você tem a probabilidade da “operação com prejuízo”, calculada no primeiro exemplo, e quer a probabilidade de ter sido disparada pelo robô A. Isto é, a probabilidade de A, dado que D ocorreu.

 Exercício 1: para a situação do segundo exemplo, calcule a probabilidade de a operação que resultou em prejuízo ter partido do robô B. Depois, calcule para o robô C.

Exercício 2: use diagramas de árvore para resolver o primeiro exemplo.

 Quando a probabilidade de um evento A ocorrer não afetar a probabilidade de outro evento B ocorrer, dizemos que A é independente de B. Mas isso significa que a probabilidade de A dado B é a própria probabilidade de A:

 Sendo assim, também vale que

 A última igualdade servirá como definição para eventos independentes.

Vamos definir o seguinte experimento: três lançamentos de uma moeda não viciada. Se usarmos X para cara e U para coroa, o espaço equiprovável é

S = {XXX. XXU, XUX, UXX, XUU, UXU, UUX, UUU }

Sejam os eventos

A = {primeiro lançamento é U},

B = {segundo lançamento é U}, e

C = {ocorre XX, isto é, exatamente duas caras consecutivas}.

Exercício 3: verifique as relações de dependência ou independência entre os três eventos listados.

No exercício 3, é fácil verificar, usando a definição matemática de independência, as relações citadas. Mas eu gostaria de que você explicasse, com palavras, cada relação.

Exemplo 1: Na próxima semana, a probabilidade de a ação A subir na próxima semana é de ¼, enquanto a probabilidade de a ação B subir é de 2/5. Sabendo que os preços dessas ações não se influenciam mutuamente, qual a probabilidade de que uma delas suba na próxima semana?

Considere A = {alta da ação A na próxima semana}, e B = {alta da ação B na próxima semana}. Desde que os eventos são independentes, temos:

 Ou seja, a probabilidade de que uma das duas suba é de 0,55, ou seja, 55%.

Exercício 4: em uma competição de tiro ao alvo, Camilo tem 1/3 de chances de acertar o alvo, enquanto Wagner tem 3/4 de chances de acertar o alvo. Se ambos atiram no alvo, qual é a probabilidade de o alvo ser atingido?

Pegando carona no nosso exercício 4, podemos formular um exemplo para falar de outro conceito, que na verdade já apareceu de forma indireta acima. É o seguinte: suponha que Wagner seja capaz de acertar o alvo com probabilidade de 0,95, e que ele atirará 30 vezes. Temos aí, um fenômeno que tem apenas dois resultados possíveis: acertar ou errar o alvo. Ainda mais, a probabilidade de acertar ou errar continuam as mesmas para cada uma das 30 repetições.

Para esse tipo de fenômeno, frequentemente chamamos um resultado de sucesso e o outro de fracasso. As probabilidades de um e de outro serão representadas, respectivamente por p e q. O número de repetições será representado por n.

Mais especificamente, se o experimento pode ser repetido um número fixo de vezes, os resultados das provas não se afetam mutuamente (são independentes), só há dois resultados possíveis (sucesso ou fracasso), e as probabilidades são constantes, estamos diante de uma distribuição de probabilidade binomial.

Por exemplo, cada lâmpada testada, de um conjunto de 5 lâmpadas selecionadas aleatoriamente em uma fábrica, acende ou não acende. Podemos dizer que 5 é o número de repetições, que o sucesso é acender e que o fracasso é não acender. Precisamos das probabilidades de acender e de não acender.

Digamos, então, que a probabilidade de acender serja 0,98 e, daí, a probabilidade de não acender é 0,02. Poderíamos estar interessados em saber qual a probabilidade de que duas das cinco lâmpadas não acendam.

Já sabemos que as provas são independentes e que podemos multiplicar as probabilidades, de sucesso (não acende) e de fracasso (acende):

(0,02)(0,02)(0,98)(0,98)(0,98) = (0,02)²(0,98)³ = 0,00038

Mas falta saber de quantas maneiras podemos retirar duas lâmpadas entre cinco.

 Agora basta multiplicar 0,00038  10 = 0,0038 ou 0,38% de chances de que duas não acendam.

Em casos desse tipo, surge uma variável aleatória (VA) X no espaço amostral S de um experimento. A VA é uma função de S no conjunto dos números reais R, tal que cada intervalo em R tem como imagem inversa um evento de S.

A partir da VA, obtemos o que se chama de distribuição de probabilidade, que também é uma função (de probabilidade) de X, definida pela associação de uma probabilidade a cada ponto de x de X(S) = {x₁, x₂, …, x_n}.

Por aqui ficamos, mas você continua com o compromisso de resolver mais exercícios sobre esse assunto. Aproveite para compartilhar seus exercícios resolvidos com seus colegas, pois Aprender é a nossa Melhor Habilidade!

Siga-me no Instagram.

Um forte abraço e até breve!

MEDIDAS DE DISPERSÃO

 É sempre um prestígio ter você aqui.

Desejo a você uma boa aprendizagem.

Nesta publicação você aprenderá sobre Desvio Médio, Variância, Desvio Padrão, e Coeficiente de Variação.

Introdução

Como você pode desconfiar pelo nome, medida de dispersão mede o quanto disperso estão os dados, ou seja, mede uma distância entre os dados.

Por exemplo, considere que um aluno tem a média em uma disciplina igual a 8. Essa informação é suficiente para que saibamos que o aluno foi aprovado naquela disciplina. Mas não sabemos se o desempenho dele foi o mesmo em todos os tópicos abordados e seria justamente essa conclusão que poderíamos ter se usássemos apenas a média aritmética. Digamos que este aluno foi submetido a 5 provas escritas, cujas notas foram usadas para calcular a média aritmética e que cada prova correspondeu a um dos tópicos apresentados. Uma medida de dispersão pode nos dar uma pista de que algum fato inusitado possa ter acontecido. No nosso exemplo, o aluno poderia ter tirado nota 10 em 4 provas e zero em uma das 5 provas que fez. A medida de dispersão vai nos ajudar a captar essa informação, embora não sejamos capazes de saber o motivo da discrepância entre as 4 notas 10 e a nota zero.

Desvio Médio

O desvio médio (DM) serve para medir a distância média entre os dados e a média e é calculado usando as seguintes expressões para dados não agrupados

Se os dados estão agrupados, inserem-se as respectivas frequências para multiplicar as diferenças entre o elemento e sua média

X é o ponto médio da i-ésima classe e f, a frequência a ele associada.

Variância

Qual é a distância de cada elemento em relação ao valor central? Quem responde a essa pergunta é a variância. A letra grega é σ² usada para representar a variância – ou segundo momento de uma distribuição – de uma população, enquanto S² representa a variância em uma amostra.

Para dados não agrupados, a variância é dada por

Em se tratando de dados agrupados, inserimos valores médios de cada classe e a respectiva frequência. O cálculo passa a ser dado por

Existe outra fórmula para calcular a variância e ela é dada a seguir:

Acima, a soma das observações A e das observações B são dadas, respectivamente, por 

A soma de seus quadrados, por 

Sendo as quantidades de valores observados de A e de B representados por η_A e η_B, nesta ordem.

Desvio Padrão

Quanto estão próximos ou distantes da média os valores que foram usados para seu cômputo? Este é o papel do desvio padrão que é obtido a partir da fórmula abaixo:

Coeficiente de Variação (CV)

Também conhecido como desvio padrão relativo (DPR) é aplicado como medida de dispersão para distribuições de probabilidade ou distribuições de frequência. Seu cálculo é feito empregando-se a fórmula:

Amplitude

A amplitude mede a diferença entre o maior e o menor valor dentre os valores observados. Logo, para calcular a amplitude, é necessário ordenar o conjunto de observações. A ordenação é uma operação estatística.

Exemplo: dadas as observações 2, 6, 10, 4, 4, 5, 7, 3, 9, 1, 1, qual seria sua amplitude? Primeiramente, ordene os dados: 1, 1, 2, 3, 4, 4, 5, 6, 7, 9, 10. Agora fica fácil reconhecer os valores máximo e mínimo das observações. Portanto a amplitude é 10 – 1 = 9.

E se os dados fossem agrupados, você acha que poderia calcular a amplitude? Como esse cálculo deveria ser feito?

Finalizamos por aqui. Foi muito bom compartilhar isso com você, pois APRENDER É A NOSSA MELHOR HABILIDADE!

Siga-me no Instagram.

Até brevíssimo!

FASES DO TRABALHO ESTATÍSTICO

 É sempre um prestígio ter você aqui.

Nesta publicação, você verá as etapas do trabalho estatístico.

Definição do Problema: qual é o seu objeto de estudo? O que você pretende resolver? Qual a informação que você quer gerar?

Planejamento: evidentemente, começa no item anterior, mas inclui outros procedimentos, tais como a definição das perguntas a serem feitas nos questionários, o cronograma da pesquisa, a população, os instrumentos que serão utilizados, as técnicas que serão aplicadas.

Coleta de Dados: ao se levantar os dados primitivos, está-se fazendo o que se chama de coleta direta, feita a partir de fontes originais. Caso a pesquisa se baseie em dados secundários, significa que a fonte não é a original, mas a partir de um banco de dados já organizado por terceiros. Por exemplo: se você visita os pluviômetros de uma região e coleta suas medições, você está fazendo uma coleta direta; caso você acesse o site da FUNCEME e colete os dados ali disponíveis, você está fazendo uma coleta indireta.

Apreciação ou Crítica: uma vez coletados, os dados devem ser verificados para levantar eventuais erros das mais variadas fontes. Tais erros podem conduzir a conclusões equivocadas sobre o fenômeno estudado. Exemplo disso, são a coleta de dados de chuva, que podem ter sido inseridos de forma errada pelo usuário (erros de digitação, etc) e podem levar a tomar decisões equivocadas sobre a gestão das águas (tanto para mais quanto para menos). Digamos que, após a análise dos dados erroneamente inseridos, concluiu-se que não era necessário um racionamento, quando na verdade era preciso racionar água. O resultado pode ser o colapso no abastecimento.

Apuração dos dados: é a fase onde se contam os dados, somando-os ou classificando-os.

Apresentação ou exposição: os resultados obtidos nas fases antecedentes são exibidos, isto é, publicados ou mostrados.

Análise e Interpretação: aqui são feitas as medidas estatísticas, como medidas de dispersão, de tendência central, de dispersão, assimetria e curtose (no caso da estatística descritiva).

Antes de seguir adiante, vamos ver o conceito de Série Estatística: trata-se de uma tabela que apresenta a distribuição de um conjunto de dados, considerando-se a época, o local, ou a espécie. Uma distribuição de frequência é a série onde os dados são agrupados em classes de acordo com as respectivas frequências. As classes são intervalos com limites predeterminados.

Exemplos:

Classes (Telefonemas recebidos)	Frequência (número de horas)		Classes (Altura de alunos em cm)	Frequência (número de alunos)
2	1		140├150	78
5	3		150├160	43
9	6		160├170	29
Total	10		Total	150

Desejo a você uma boa aprendizagem!

Compartilhe conhecimento, pois Aprender é a nossa melhor habilidade!

Siga-me no Instagram.

Até brevíssimo!

Adaptado de:

Pinnto, Marcos. Estatística Básica: para quem não é especialista. 2a ed., Fortaleza, 918641, 2021.